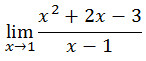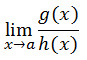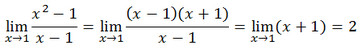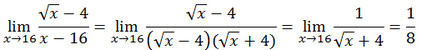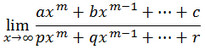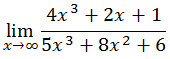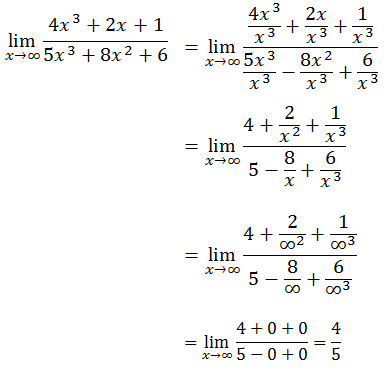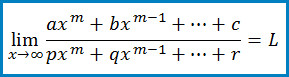Apa itu Limit Matematika?

Limit suatu fungsi f(x) untuk x mendekati suatu bilangan a adalah nilai pendekatan fungsi f(x) bilaman x mendekati a

Misalnya

ini berarti bahwa nilai dari fungsi f(x) nilainya mendekati M jika nilai x mendekati abiar lebih paham kita simak contoh berikut

Contoh 1
Tentukan limit dari

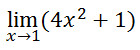
Jawab :
Untuk nilai x mendekati 1 maka (4×2+1) akan mendekati .12 + 1 = 5 sehingga nilai dari

Contoh 2
Tentukan nilai dari limit

Jawab
Misal sobat langsung memasukkan nili x = 1 ke dalam persamaan hasilnya tidak akan terdefinisi karena bilangan pembagi ketemu 0 (x-1). Akan tetapi bentuk di atas masih bisa disederhakan guna menghilangkan komponen pembagi yang bernilai nol yaitu

Cara Mengerjakan Limit Fungsi yang Tidak Terdefinisi

Adakalanya penggantian niali x oleh a dalam lim f(x) x→a membuat f(x) punya nilai yang tidak terdefinisi, atau f(a) menghasilkan bentuk 0/0, ∞/∞ atau 0.∞. Jika terjadi hal tersebut solusinya adalah bentuk f(x) coba sobat sederhanakan agar nilai limitnya dapat ditenntukan.

Limit Bentuk 0/0

---

Bentuk 0/0 kemungkinan timbul dalam

ketika sobat menemukan  bentuk seperti itu coba untuk utak-utik fungsi tersebut hingga ada yang bisa dicoret. Jika itu bentuk persaman kuadrat sobat bisa coba memfaktorkan atau dengan cara asosiasi dan jangan lupakan ada aturan a²-b² = (a+b) (a-b). Berikut contohnya

Bentuk ∞/∞

---

Bentuk limit  ∞/∞ terjadi pada fungsi suku banyak (polinom) seperti

Contoh Soal
Coba sobat tentukan

Jawab

Berikut rangkuman rumus cepat limit matematika bentuk  ∞/∞

Rumus Trigonometri 

 

Rumus Jumlah dan Selisih Sudut

Dari gambar segitiga ABC berikut:

AD = b.sin α
BD = a.sin β
CD = a.cos β = b.cos α

Untuk mencari cos(α+β) = sin (90 – (α+β))°

Untuk fungsi tangens:

Sehingga, rumus-rumus yang diperoleh adalah:

Rumus Sudut Rangkap

Sehingga, rumus-rumus yang diperoleh adalah:

Penurunan dari rumus cos2α:

Rumus Perkalian Fungsi Sinus dan Kosinus

Dari rumus-rumus jumlah dan selisih dua sudut dapat diturunkan rumus-rumus baru sebagai berikut:

Sehingga, rumus-rumus yang diperoleh:

Rumus Jumlah dan Selisih Fungsi Sinus dan Kosinus

Dari rumus perkalian fungsi sinus dan kosinus dapat diturunkan rumus jumlah dan selisih fungsi sinus dan kosinus.

Maka akan diperoleh rumus-rumus:

Contoh-contoh soal:
(1) Tanpa menggunakan daftar, buktikan bahwa:

(2) Buktikan bahwa dalam segitiga ABC berlaku:

 

Rumus Pythagoras Serta Penerapannya

 

Rumus matematika yang sangat familiar dikalangan pelajar yaitu rumus pythagoras, bagi sobat semua juga pastinya sudah tidak asing lagi. Pengertian dari rumus pythagoras yaitu rumus yang digunakan untuk mencari panjang sisi pada sebuah segitiga siku-siku. Apa itu segitiga siku? yaitu segitiga yang salah satu sudutnya memiliki besar 90°.

Untuk membuktikan rumus pythagoras / teorema pythagoras diatas, sebenarnya terdapat banyak cara. Pada kesempatan kali ini akan kita gunakan cara sederhana untuk membuktikannya. Jika kita mempunyai segitiga siku-siku, cobalah disusun sehingga membentuk sebuah persegi seperti gambar dibawah ini.

Luas Persegi Besar = Luas Persegi

Luas Persegi Besar = luas persegi putih Kecil + Luas 4 Segitiga
(a+b)² = c² + 1/2ab+1/2 ab+1/2 ab +1/2 ab

                             (a+b)² = 2 ab
         a² + 2ab + b² = c² + 2ab

          a² +b² = c²

Pembuktian teorema pythagoras yang lain dapat sobat lakukan langsung dirumah, jika rumah sobat menggunakan lantai ubin atau keramik. Cobalah buat segitiga dengan alas 4 keramik dan tinggi 3 keramik, seperti gambar dibawah ini.

Jika sudah, silahkan sobat hitung panjang sisi miring yaitu garis yang diberi tanda warna merah. Jika sobat semua benar dalam menghitungnya akan diperoleh hasil panjang sisi miring yaitu 5 kali panjang ubin/ keramik.
Dalam kehidupan nyata rumus pythagoras banyak pemanfaatannya, salah satu contohnya yaitu pada bidang arsitektur. Seorang arsitek akan menggunakan rumus pythagoras dalam menentukan kemiringan suatu bangunan misalnya saja kemiringan sebuah tanggul agar tanggul tersebut dapat menahan tekanan air. Contoh lainnya yaitu seorang tukang kayu, ketika dia membuat segitiga penguat pilar dia menggunakan rumus pythagoras.
Perhatikan contoh soal dibawah ini :
1.  Jika diketahui BC = 8cm, AC = 6cm. Berapakah panjang sisi AB pada gambar di bawah ini ?

Jawab:
AB² = AC² + BC²
= 6² + 8²
= 36 + 64
= 100AB
= √100
= 10
Jadi panjang sisi AB adalah 10cm.
2. Berapakah panjang sisi a pada gambar di bawah ini ?

Jawab:
Karena yang ditanyakan adalah panjang sisi a , maka berlaku rumus:
a² = c² – b²
= 17² – 8²
= 289 – 64 = 225
a = √225 = 15 cm

 

 Sejarah Matematika


Cabang pengkajian yang dikenal sebagai sejarah matematika adalah penyelidikan terhadap asal mula penemuan di dalam matematika dan sedikit perluasannya, penyelidikan terhadap metode dan notasi matematika pada masa silam.
Sebelum zaman modern dan penyebaran ilmu pengetahuan ke seluruh dunia, contoh-contoh tertulis dari pengembangan matematika telah mengalami kemilau hanya di beberapa tempat. Tulisan matematika terkuno yang telah ditemukan adalah Plimpton 322(matematika Babilonia sekitar 1900 SM)^, Lembaran Matematika Rhind (Matematika Mesir sekitar 2000-1800 SM) dan Lembaran Matematika Moskwa (matematika Mesir sekitar 1890 SM). Semua tulisan itu membahas teorema yang umum dikenal sebagai tearima Phitagoras, yang tampaknya menjadi pengembangan matematika tertua dan paling tersebar luas setelah aritmetika dasar dan geometri.
Sumbangan matematika Yunani memurnikan metode-metode (khususnya melalui pengenalan penalaran deduktif dankekakua matematika di dalampembuktian matematika) dan perluasan pokok bahasan matematika. Kata "matematika" itu sendiri diturunkan dari kata Yunani kuno, μάθημα (mathema), yang berarti "mata pelajaran". Matematika Cina membuat sumbangan dini, termasuk notasi poposional. Sistem bilangan Hindu Arab dan aturan penggunaan operasinya, digunakan hingga kini, mungkin dikembangakan melalui kuliah pada milenium pertama Masehi di dalam matemaka India dan telah diteruskan ke Barat melalui matematika Islam,pada gilirannya, mengembangkan dan memperluas pengetahuan matematika ke peradaban ini. Banyak naskah berbahasa Yunani dan Arab tentang matematika kemudian diterjemahkan ke dalam bahasa Latin, yang mengarah pada pengembangan matematika lebih jauh lagi di Zaman pertengahan Eropa
Dari zaman kuno melalui Zaman Pertengahan, ledakan kreativitas matematika seringkali diikuti oleh abad-abad
kemandekan. Bermula pada abad Reinaisans Italia pada abad ke-16, pengembangan matematika baru,
berinteraksi dengan penemuan ilmiah baru, dibuat pada pertumubuhan esposional yang berlanjut hingga kini.